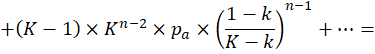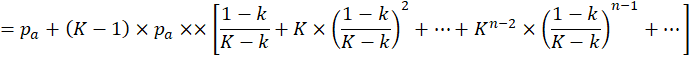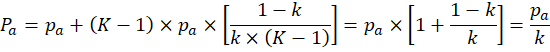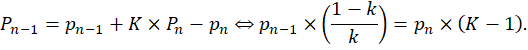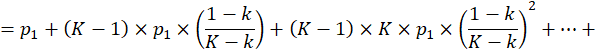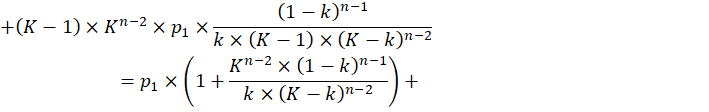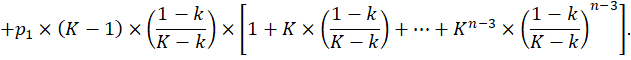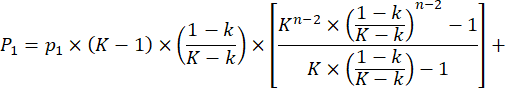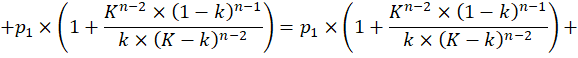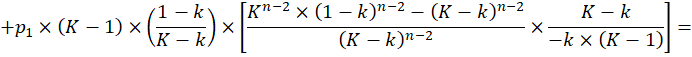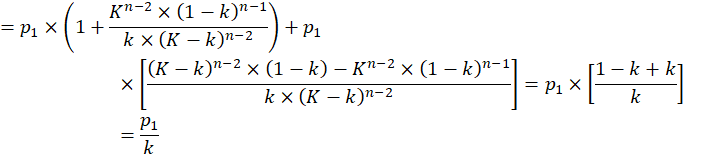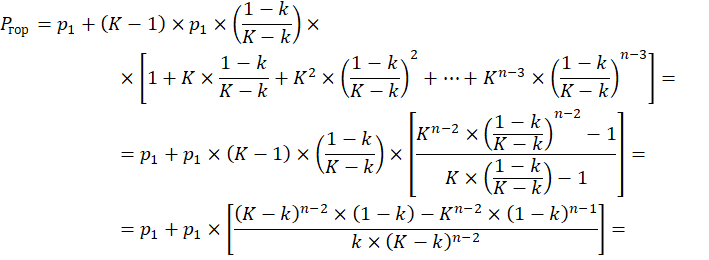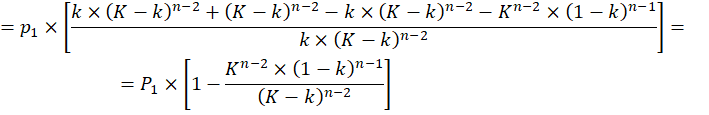RURAL POPULATION OF CENTRAL PLACE SYSTEMS
JOURNAL: « GEOPOLITICS AND ECOGEODYNAMICS OF REGIONS» Volume 7 (17) issue 3, 2021
Section 1. Theoretical aspects of geopolitics and ecogeodynamics
Publication text (PDF):Download
UDK: 911.8
AUTHOR AND PUBLICATION INFORMATION
AUTHORS:
- R. V. Dmitriev, Institute of Geography RAS; Institute for African Studies RAS, Moscow, Russian Federation
- S. A. Gorokhov, Institute of Geography RAS, Moscow, Russian Federation
TYPE: Article
DOI: 10.37279/2309-7663-2021-7-3-26-33
PAGES: from 26 to 33
STATUS: Published
LANGUAGE: Russian
KEYWORDS: central place theory, rural population, hierarchy level, settlement continuum, isolated grid, rural population share.
ABSTRACT (ENGLISH): The main quantitative indicator of the Central Place Theory (CPT), which makes it possible to put forward many of its provisions, is the share of the central place in the population of the area it serves (k). Earlier, we proposed a complete version of the proof of the constancy of k for all hierarchical levels for any values of k, and also established an upper bound for their set in the form of a nonstrict invariant. However, what is k in itself? At first glance, the answer is obvious: this parameter is the quotient of dividing the population of the central place by the population of the area it serves. At the same time, what population size should be taken for consideration? All domestic and foreign studies within the CPT proceed from the assumption that, comparing theory with empirical reality, we should consider urban settlement systems not as closed systems, but as fragments of the settlement continuum. The article examines the phenomenon of uniform distribution of the rural population in the systems of central places. It is shown that in the works of our predecessors, the systems of central places were actually considered not as part of a continuous and infinite continuum of settlement, but as independent systems. It has been established that within the isolated systems of central places, the rural population is not distributed evenly, but in the corresponding hierarchical settlements. An equation is derived for the dependence of the share of the rural population in the total population of the system on the fundamental parameters of the latter:
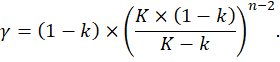
Thus, for isolated systems, the total population includes the number of not only the central places, but also the rural population. At the same time, we substantiated the possibility of the existence of such within isolated areas – within state borders or, for example, on the islands. Consideration of the latter was undertaken by researchers earlier, however, the possibility of their existence was not proved and, as a result, their consideration from the point of view of the CPT was not substantiated.
Введение
Все отечественные и зарубежные исследования в рамках теории центральных мест (ТЦМ) (к примеру, [1; 2; 3; 4; и др.]) исходят из положения, что, «сопоставляя теорию с эмпирической реальностью, мы должны рассматривать системы городского расселения не как закрытые системы, а как фрагменты континуума расселения» [5, с. 85]. Это же относится и к сельскому населению: оно, будучи размещенным равномерно — в соответствии с самой ТЦМ — создает «некоторую несамосогласованность теории Кристаллера–Лёша (применительно к размещению городских поселений)», поскольку «территории, расположенные ближе к городу, обычно характеризуются более высокой интенсивностью использования земли, более высокой плотностью населения» [6, с. 40]. Попытаемся преодолеть указанную несамосогласованность.
Материалы и методы
Главный количественный показатель в ТЦМ, обеспечивающий возможность выдвижения многих ее положений — доля центрального места в населении обслуживаемой им зоны (k). Насколько нам известно, впервые гипотеза о постоянстве значения k для всех уровней иерархии была выдвинута в [5]. Ее доказательство производилось путем перебора некоторых значений, однако не охватывало всего их множества — следовательно, оно не может считаться полным. В [7] нами предложен полный вариант доказательства для любых значений k, а также установлена верхняя граница их множества в виде нестрогого инварианта. Однако что же есть k само по себе? На первый взгляд, ответ очевиден: этот параметр представляет собой частное от деления численности населения центрального места на численность населения обслуживаемой им зоны. В то же время какую численность населения брать для рассмотрения, если решетка бесконечна — в соответствии с классической ТЦМ?
В кристаллеровском варианте теории число центральных мест на любом уровне иерархии под номером n > 1 равно (K-1)*Kn-2, где К — число центральных мест данного уровня иерархии, обслуживаемых одним центральным местом более высокого уровня, уменьшенное на единицу (уровни нумеруются сверху). Представим, что численность населения некоего «участка» решетки равна (вернее, для бесконечной решетки — стремится к, если последовательность сходится) некоему Pa и выразим ее через численность населения только лишь входящих в него центральных мест. Начнем с некоего уровня a:
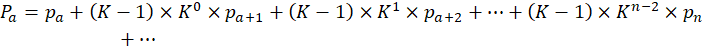 |
(1) |
Применяя уравнение Бекманна-Парра выразим в (1) численность населения каждого центрального места через pa:
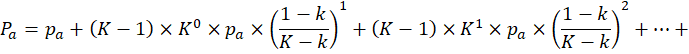
|
(2) |
Очевидно, выражение в квадратных скобках представляет собой сумму членов бесконечно убывающей геометрической прогрессии со знаменателем ![]() . Тогда (2) может быть приведено к виду:
. Тогда (2) может быть приведено к виду:
Само по себе полученное выражение соответствует аксиоматике ТЦМ и не представляет собой чего-то экстраординарного — за исключением того, как оно было выведено. Из последовательности вычислений становится понятно, во-первых, почему сельское население, не будучи размещенным в иерархических поселениях, в определенной степени «вынужденно» расселяется в рамках всего оставшегося пространства классической кристаллеровской решетки — у него просто не остается иного «выбора», и его расселение должно иметь равномерный пространственный характер. Во-вторых, если мы хотим перейти к выявлению соответствия реальных систем расселения теоретическим построениям [8], то, рассматривая определенную часть бесконечной решетки и учитывая не-вхождение сельского населения в формулы, мы вынужденно приходим к необходимости не только что-то делать с самым последним уровнем иерархии (k для которого не равно таковому для всех вышележащих уровней), но и — что крайне важно! — должны для установления значения k всех уровней (кроме последнего, взятого для рассмотрения) поделить численность населения центрального места первого уровня на численность населения не всего анализируемого участка решетки, а только лишь системы центральных мест, располагающихся в его пределах без учета сельского населения.
Учитывая приведенные выше расчеты, мы приходим к выводу, что заключения наших предшественников могли быть не совсем верными: в рамках классической ТЦМ, имеющей дело с бесконечной решеткой, население всего рассматриваемого ее участка (P) включает только население собственно центральных мест без учета сельского населения.
Результаты и обсуждение
Подойдем к рассмотрению этого вопроса с несколько иной стороны, взяв для рассмотрения изолированную систему центральных мест — островную или замкнутую границами, то есть, в конечном счете, развивающуюся относительно самостоятельно вне общего континуума расселения. Пусть данная система имеет n уровней иерархии — от первого, представленного одним центральным местом, до уровня под номером n, представленного только сельскими населенными пунктами, которые обслуживают только самих себя и не имеют собственных заселенных дополняющих районов (уровни нумеруются сверху). Тогда для одной зоны n-го уровня Pn = pn. Тогда получаем:
В этом случае уравнение Бекманна-Парра, связывающее численность населения предпоследнего и последнего уровней иерархии, будет иметь вид:
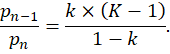 |
(4) |
Уравнение (4) было получено в [9]. Очевидно, k в данном случае равно k для всех остальных уровней иерархии. Соотношение же численности населения 1-го и n-го уровней составляет:
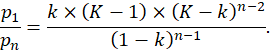 |
(5) |
Для n-го уровня k=1, что ни в коей мере не противоречит общим положениям теории — нам нужно будет лишь ввести в них соответствующее пояснение. Теперь попытаемся установить, как же вычислить k для изолированных систем центральных мест — вернемся к уравнению (1). В этом случае оно сохраняет свой вид для n уровней иерархии, за исключением многоточия в конце, поскольку изолированная система конечна. Учитывая это, а также (4) и (5), перепишем (1):
Выражение в квадратных скобках представляет собой сумму членов геометрической прогрессии со знаменателем ![]() Тогда, продолжая определять P1, имеем:
Тогда, продолжая определять P1, имеем:
Теперь подойдем к рассмотрению изолированных систем центральных мест с другой стороны и выясним, происходит ли их эволюция по схожему с бесконечной решеткой сценарию [10] или же имеет свои особенности. Для этого вернемся к уравнению (2), переписав его только лишь для городских поселений — без учета сельских населенных пунктов последнего уровня n:
Разделив левую и правую части на P1, получаем:
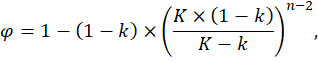 |
(6) |
где j – доля городского населения.
Полученное для конечной решетки уравнение (6) отличается от такового для бесконечной решетки [10] лишь показателем степени, уменьшенным на единицу. Это вполне объяснимо: в бесконечной решетке показатель степени равен n–1, поскольку мы берем в качестве «стартового» лишь одно место условно первого уровня, ограничивая решетку сверху. Ограничивая решетку и снизу — то есть делая ее окончательно изолированной — мы «убираем» центральные места последнего иерархического уровня: n в нашем случае включает и первый уровень, представленный одним центральным местом (вычитаем «1» из n), и последний, включающий сельские населенные пункты (вычитаем еще раз «1» из n). В конечном счете, из (6) получаем следующее выражение для вычисления доли сельского населения (g)в изолированной решетке центральных мест:
Выводы
Таким образом, для изолированных систем центральных мест P1 включает в себя численность не только собственно центральных мест, но и сельского населения. Последнее в этом случае размещено не равномерно, а тяготеет к тому или иному центральному месту в той степени, в какой это центральное место велико по численности своего населения, то есть больше или меньше другого. Иными словами, во всех работах наших предшественников системы центральных мест на самом деле рассматривались НЕ как часть континуума расселения, а именно как самостоятельные системы. При этом нами обоснована возможность существования таковых в рамках изолированных участков — в пределах государственных границ или к примеру, на островах. Рассмотрение последних было предпринято и ранее [11], однако не была доказана возможность их существования и, как следствие, не было обосновано их рассмотрение с позиции ТЦМ.
REFERENCES
- Valesjan A. L. Sinhronnost’ v prostranstvennoj jevoljucii sistem rasselenija i transportnyh setej: Doctor’s thesis. , 1995. 232 p. (in Russian)
- Hudjaev I. A. Jevoljucija prostranstvenno-ierarhicheskoj struktury regional’nyh sistem rasselenija: candidate’s thesis. , 2010. 161 p. (in Russian)
- Shuper V. A. Ustojchivost’ prostranstvennoj struktury sistem gorodskogo rasselenija: Doctor’s thesis. , 1990. 223 p. (in Russian)
- Parr J. B. City Hierarchies and the Distribution of City Size: a Reconsideration of Beckmann’s Contribution, Journal of Regional Science. 1969. Vol. 9, 2. pp. 239–253.
- Shuper V. A. Samoorganizacija gorodskogo rasselenija. M.: Rossijskij otkrytyj universitet, 1995. 168 p. (in Russian)
- Gusejn-Zade S. M. Modeli razmeshhenija naselenija i naselennyh punktov. M.: Izd-vo MGU, 1998. 92 p. (in Russian)
- Dmitriev R. V. K voprosu o postojanstve znachenija doli central’nogo mesta v naselenii obsluzhivaemoj im zony dlja vseh urovnej kristallerovskoj ierarhii, Izvestija Rossijskoj akademii nauk. Serija geograficheskaja. 2019. 1. pp. 128–135. (in Russian)
- Gorohov S. A., Dmitriev R. V. Paradoksy urbanizacii sovremennoj Indii, Geografija v shkole. 2009. 2. pp. 17–23. (in Russian)
- Arhipov Ju. R. Sistemnoe modelirovanie regional’nogo rasselenija: dis. … d-ra geogr. nauk. M., 2002. 342 p. (in Russian)
- Dmitriev R. V. Jevoljucija sistem rasselenija v aspekte klassicheskoj teorii central’nyh mest, Izvestija Rossijskoj akademii nauk. Serija geograficheskaja. 2021. Vol. 85, 2. pp. 165–167. (in Russian)
- Vazhenin A. A. Primenimost’ teorii central’nyh mest k izucheniju sistem rasselenija na ostrovah, Izvestija Rossijskoj akademii nauk. Serija geograficheskaja. 2008. 2. pp. 7–12. (in Russian)