АЛГОРИТМ КАЛИБРОВКИ ФОТОГРАММЕТРИЧЕСКИХ ПАРАМЕТРОВ ДЛЯ РАСЧЁТА ТРЁХМЕРНЫХ КООРДИНАТ ТОЧЕК ИЗОБРАЖЕНИЯ

27.12.2024 | by gudilin gudilin |

*УДК 528.8*
Рихтер А. А.^1,2, Чуклин С. И.^2,3	*Алгоритм калибровки фотограмметрических параметров для расчёта трёхмерных координат точек изображения*

	¹Акционерное общество «Тазмар АйТи-солюшнз», г. Санкт-Петербург² Научно-исследовательский институт аэрокосмического мониторинга “АЭРОКОСМОС”, г. Москва ³ ФГБОУ ВО «Санкт-Петербургский государственный университет», г. Санкт-Петербург e-mail: ¹urfin17@yandex.ru

Аннотация. В работе описан алгоритм предварительной калибровки фотограмметрических параметров для возможности практического применения фотограмметрической модели преобразования «плоских» координат точек снимка в соответствующие трёхмерные координаты точек объекта. Представлена общая схема алгоритма, состоящего из пяти шагов. Для описания процедур условно вводятся понятия базиса изображения (первичного и калиброванного) и вида. Входными данными алгоритма являются набор обучаемых образцов, каждый из которых включает само изображение (с наличием необходимых метаданных) и их эталонные полигоны (в виде географических координат вершин изображения). Проведён эксперимент по калибровке на примере обучаемого набора в составе общедоступного датасета. Для произвольного тестового изображения в составе датасета проведена калибровка фотограмметрических параметров и рассчитаны трёхмерные координаты на примере характерных точек изображения.

Ключевые слова: калибровка, фотограмметрические параметры, трёхмерные координаты.

Введение

Существует большое количество фотограмметрических методов, описывающих структурные и геометрические характеристики изображённых объектов [1-4]. Они имеют широкий спектр применимости в задачах компьютерного зрения [5-6].

Один из методов описывает стандартное преобразование координат из систем координат стереопары (левого и правого снимка) в систему координат объекта. Применение «напрямую» фотограмметрической модели преобразования координат изображения в координаты объекта нецелесообразно, ввиду того, что параметры внешнего и внутреннего ориентирования снимков не откалиброваны. В литературе встречаются методики калибровки фотограмметрических параметров [7-8]. Многие из них сложны в описании и технической реализации. Методы фотограмметрии, в том числе методы калибровки, описанные в соответствующей литературе, часто понятны специалистам по фотограмметрии, но не исследователям, для которых поставлена задача, связанная с геометрической интерпретацией изображённых объектов.

В данной работе предлагается алгоритм калибровки фотограмметрических параметров для практических расчётов трёхмерных координат изображённых объектов по их матричным координатам (в матрице изображения).

Описание алгоритма

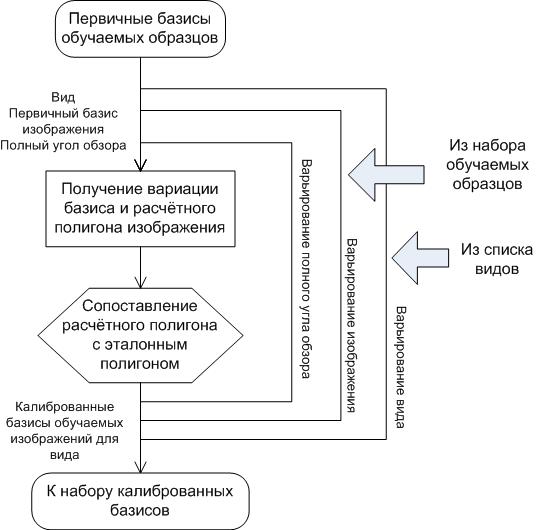
Общая схема алгоритма калибровки проиллюстрирована на рисунке 1.

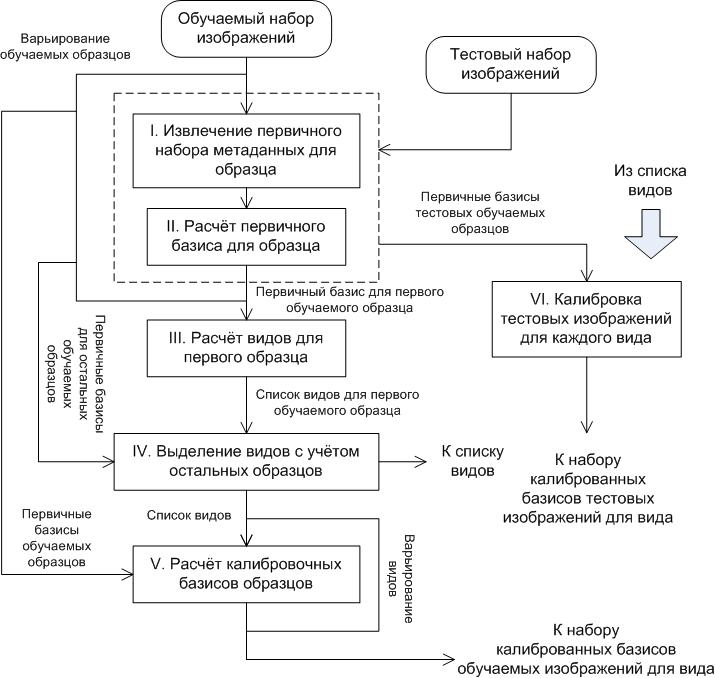Рис. 1.Общая схема алгоритма калибровкиСоставлено авторами

Входными данными является набор обучаемых образцов:

где – число образцов, i – номер образца, – i-е эталонное изображение, – соответствующий -й эталонный полигон (полигон соответствующего изображения, покрывающий изображённую территорию).

Эталонные изображения в составе набора получены съёмкой земной поверхности с одной камеры с постоянными техническими условиями съёмки.

Эталонный полигон задаётся в виде (рисунок 2):

– географические координаты -го угла -го обучаемого изображения (-й вершины полигона); – матричные координаты соответствующих точек (номер строки, номер столбца).

«» – обозначение географических координат геометрического объекта , «- обозначение картографических координат (в проекции UTM), «» – обозначение матричных координат .

Из рисунка 2: – верхний левый угол, ; – нижний левый угол, ; – нижний правый угол, ; – верхний правый угол, . Параметры и – размеры изображения в пикселях.

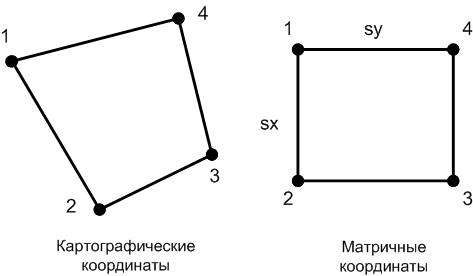Рис. 2. Эталонный полигонСоставлено авторами

Обозначим преобразование географических координат точки земной поверхности в картографические координаты , которое считается общеизвестным [9]:

где – номер зоны, – код EPSG (для географических координат код EPSG равен ). Аппликата в точке определяется, исходя из цифровой модели рельефа (ЦМР), местности (ЦММ) или поверхности (ЦМП), либо считается постоянной в окрестности точки фотографирования и прописывается в метаданных (см. далее параметр ).

Обратное преобразование можно получить по формуле:

Опишем этапы работы алгоритма калибровки фотограмметрических параметров.

Первичный набор необходимых метаданных, извлекаемый с изображения, представлен в таблице 1. Обозначены примеры ключа для тега, по которому можно найти соответствующие метаданные.

Таблица 1

Первичный набор метаданных

№	Названия [единица измерения]	Обозначения	Примеры ключей
1	Высота [пк]		«image», «height»
2	Ширина [пк]		«image», «width»
3	Реальное (истинное) фокусное расстояние камеры [м]		«focal», «length»
4	Фокусное расстояние в полнокадровом эквиваленте [м]		«35», «mm»
5	Широта положения камеры [рад]		«gps», «latitude»
6	Долгота положения камеры [рад]		«gps», «longitude»
7	Абсолютная высота над уровнем моря точки фотографирования [м]		«abs», «altitude»
8	Высота относительно поверхности Земли точки фотографирования [м]		«rel», «altitude»
9	Угол рыскания положения камеры [рад]		«yaw», «degree»
10	Угол тангажа положения камеры [рад]		«pitch», «degree»
11	Угол крена положения камеры [рад]		«roll», «degree»

Составлено авторами

Если некоторый угловой параметр задан в градусах / минутах / секундах , то он переводится в радианы по формуле:

II. Базис изображения – набор параметров, извлекаемый и рассчитанный из первичного набора метаданных, применяемый на практике при фотограмметрической обработке изображений.

Первичный базис изображения задаётся параметрами 1-10 (таблица 2): . Получение первичного базиса изображения обозначим .

Таблица 2

Состав первичного базиса

№	Название параметра	Обозначение
1	Матричные координаты главной точки [пк]
2	Размеры изображения [пк]
3	Географические координаты точки фотографирования [рад]	,
4	Картографические координаты точки фотографирования [м]
5	Относительная высота точки фотографирования [м]
6	Фокусное расстояние [м]
7	Углы Эйлера положения камеры [рад]
8	Полные углы обзора [рад]
9	Матрица поворота	A
10	Зона координатной проекции

Составлено авторами

Параметры 2-3, 5-7 остаются, как в таблице 1. Параметры 1, 8 могут не храниться в метаданных изображения и рассчитываются по алгоритму, приведённому ниже.

Параметры 4:

Полные углы обзора по вертикали и горизонтали можно вычислить по формулам [10]:

; . (1)

и – высота и ширина сенсора полного кадра [м], и – высота и ширина сенсора в полнокадровом эквиваленте [мм], – фокусное расстояние объектива, используемого с сенсором меньшего формата [м], – фокусное расстояние объектива с таким же углом зрения на 35 мм (полного кадра) [м], – множитель фокусного расстояния, равный также так называемому кроп-фактору. Высота и ширина сенсора полного кадра: .

Параметр 9 [3]:

где , т.е. .

III. Вид – истинное направление на изображённую поверхность, определяемый набором параметров:

– вектор смещений на «прямые» углы углов Эйлера :

– вектор направлений смещений углов:

– вектор порядков углов: .

Корректируемые углы Эйлера для определённого вида и изображения (образца ):

– соответствующие углы Эйлера в первичном базисе изображения .

На рисунке 3 приведена схема расчёта видов для первого образца.

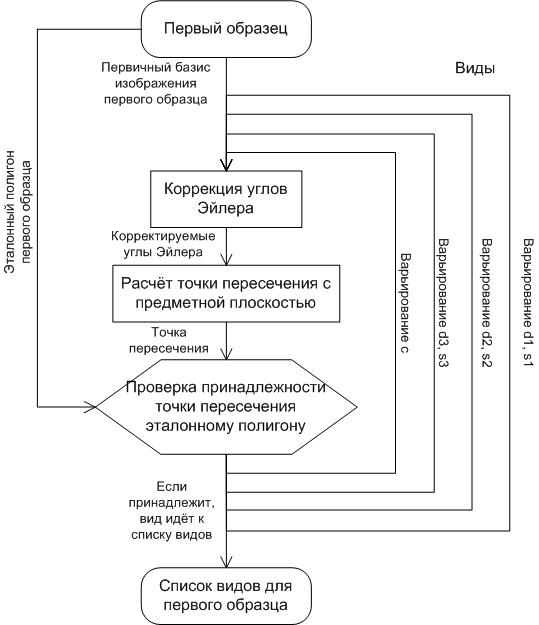Рис. 3. Схема получения видов по первичным базисам для первого образцаСоставлено авторами

На рисунке 4 показано соотношение предметной плоскости и истинного направления , исходящего из точки и образованного углами , на изображённую поверхность . – картографическая система координат, – система координат изображения . [11-12]

Плоскость образована точками полигона (для -го образца). Если неровностью местности пренебрегать, то и является предметной плоскостью с уравнением , где – высота поверхности Земли над уровнем моря в точке .

По правилам аналитической геометрии:

, , (2)

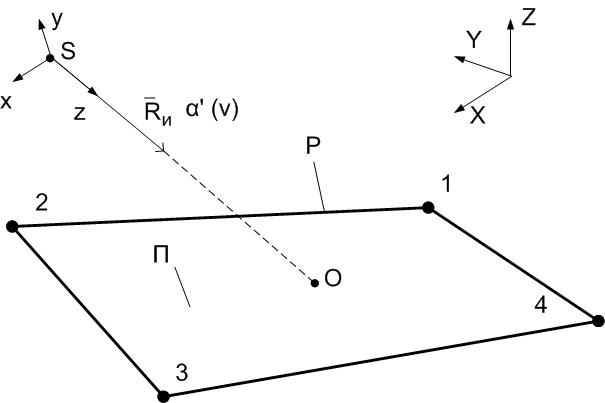Рис.4.Истинное направление на предметную плоскость (для -го образца и вида )Составлено авторами

Рис. 5. Схема получения видов по первичным базисам для остальных образцовСоставлено авторами

– нормированный вектор вдоль оси в системе координат . По (2) находятся координаты точки – проекции главной точки изображения на предметную плоскость. Далее по алгоритму «точка в полигоне» [13] проверяется принадлежность точки полигону . Если

, (3)

соответствующий вид поступает в список видов для первого образца.

При формировании списка видов учитывается встречаемость одинаковых направлений . И если для очередного направление , оно повторно не ходит в список .

IV. На рисунке 5 приведена схема расчёта видов для остальных образцов. Для каждого вида из по всем остальным образцам и их первичным базисам находятся точки , проверяется их принадлежность соответствующим полигонам . Если для данного вида условие (3) выполняется, то остаётся в списке . Если для данного вида , для которого условие (3) не выполняется, то удаляется из списка .

Чем больше число обучающих образцов и чем более отличительные ракурсы съёмки (углы Эйлера), тем меньше элементов в – в пределе один элемент.

V. На рисунке 6 приведена схема расчёта калибровочных базисов обучаемых изображений по первичным базисам для каждого вида из рассчитанного списка видов.

Рис. 6. Схема расчёта калибровочных базисов обучаемых изображений по первичным базисам и видамСоставлено авторами

Вариации базисов задаются параметрами (см. таблицу 2): (штрихами обозначены отличающиеся параметры от ). Данное преобразование обозначим: .

Так как технические условия съёмки постоянны, то считаются постоянными для всех -х образцов. Если не удалось рассчитать по формуле (1), они варьируются на множестве , заданном интервально, например, от 1^o до 45^o с шагом 0.1^o. Из (1) можно записать:

В этом случае находятся при минимуме суммарных отклонений расчётных полигонов от соответствующих эталонных полигонов для данного вида :

. (4)

– координаты -й точки эталонного полигона -го образца, – координаты -й точки расчётного полигона -го образца.

На рисунке 7 показана пояснительная схема вычисления картографических координат точек расчётного полигона для изображения , а также матричных координат главной точки изображения. – плоскость, параллельная наклонному снимку, – плоскость, параллельная горизонтальному снимку в картографической системе координат.

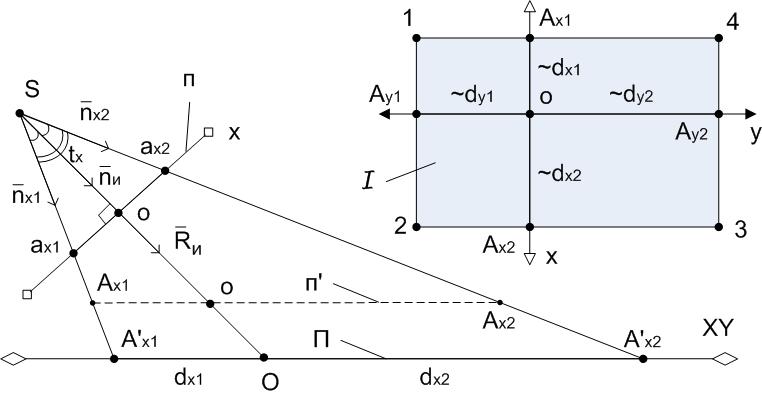Рисунок 7 – Пояснительная схема вычисления расчётного полигона (для -го образца и вида )

Для данного вида вектор рассчитывается по формуле (2).

Нормированные вектора и в системе координат (в плоскости, перпендикулярной ):

, .

Нормированные вектора и в системе координат (в плоскости, перпендикулярной ):

, .

Полигон образован точками . В системе координат точки находятся по формуле (см. формулу (2) и рисунок 7):

, ,

где индекс «*» для краткости обозначает одно из .

Тогда .

Координаты точки рассчитываются с учётом следующего: 1) приведение суммы отклонений вдоль осей и к единице; 2) приведение сумм к размерам изображения; 3) приведение координат точки к нулевому значению. В этом случае:

. (5)

Фотограмметрическая модель расчёта картографических координат по матричным координатам [12-13]:

, (6)

, , ,

– приведённое значение фокусного расстояния.

Координаты точек 1-4 (вершин полигона ) рассчитываются по данной модели: . Переход в географические координаты: . Если и не были вычислены по формуле (1), то значения данных координат подставляются в формулу (4) для оценки оптимальных и по множеству изображений для одного вида .

Для каждого вида калибровочные базисы изображений – вариации базисов, при которых вычислены по формуле (4) и по формуле (5).

VI. По результатам выполнения шагов I-II, V находятся калиброванные базисы для произвольных других изображений , снятых с той же камеры (тестовых образцов), по рассчитанным видам и их соответствующим первичным базисам .

Для тестовых изображений картографические и географические координаты точки изображения рассчитываются по формулам при известной одной из картографических координат (см. формулу (6)):

– при известной абсциссе точки:

, (7)

;

– при известной ординате точки:

, (8)

;

– при известной аппликате точки:

, (9)

;

где: , , , , .

Проведение эксперимента

Представим результаты работы данного алгоритма на примере изображений ортофотопланов в составе датасета Terrain Creator, полученного с беспилотного летательного аппарата [14].

В таблице 3 отражены обучаемые образцы: ID эталонных изображений , взятых с датасета; географические координаты точек их эталонных полигонов (угловых точек на изображениях). Последние считаются известными для , например, могут быть оценены вручную визуальным сопоставлением координат данных точек на спутниковых картах.

Таблица 3

Обучаемые образцы

i	ID изображения
1	DJI_20221115144137_0005_V	29.8886896729.88828351 29.88828546 29.88869161	98.5483839998.54838175 98.54791568 98.54791791
2	DJI_20221115144142_0008_V	29.8886859529.88827971 29.88828095 29.88868719	98.5480860198.54808459 98.54761843 98.54761985
3	DJI_20221115144145_0010_V	29.8886820829.88827587 29.88827817 29.88868367	98.5478886998.54788645 98.54742073 98.54742296

Составлено авторами

В частности, на рисунке 8 показано обучаемое изображение , в таблице 4 – его первичный набор метаданных (шаг I).

Рис. 8. Изображение 1-го обучаемого образцаСоставлено авторами

Таблица 4

Первичный набор метаданных для 1-го обучаемого образца

№	Обозначения	Значения	Тег
1		3956 пк	ExifImageHeight
2		5280 пк	ExifImageWidth
3		12.29 мм	FocalLength
4		24 мм	FocalLengthIn35mmFilm
5		[29.0, 53.0, 18.5551] град	GPSLatitude
6		[98.0, 32.0, 53.3392] град	GPSLongitude
7		394.429 м	AbsoluteAltitude
8		45.015 м	RelativeAltitude
9		-89.5 град	GimbalYawDegree
10		-90.0 град	GimbalPitchDegree
11		180.0 град	GimbalRollDegree

Составлено авторами

В таблице 5 показаны первичные базисы обучаемых образцов – см. таблицу 2 (шаг II). Так как и известны, полные углы обзора в данном случае вычислены по формуле (1).

Таблица 5

Первичные базисы обучаемых образцов

№
1	0, 0	0, 0	0, 0
2	3956, 5280	3956, 5280	3956, 5280
3	29.88848752777777798.54814977777778	29.88848341666666698.54785216666666	29.88847991666666598.54765394444445
4	456371.221655865673306514.7000242453 394.429	456342.4834707893306514.3574492577 394.434	456323.342229004253306514.044904919 394.381
5	45.015	45.023	44.981
6	0.01229	0.01229	0.01229
7	-1.562069680534925-1.5707963267948966 3.141592653589793	-1.5638150097869192-1.5707963267948966 3.141592653589793	1.5795229730548683-1.5690509975429023 0.0
8	0.46364760900080610.6435011087932844	0.46364760900080610.6435011087932844	0.46364760900080610.6435011087932844
9	[[1.2192567064669045e-16,-6.229870079406139e-17, -1.0], [0.9999619230641713, -0.008726535498373897, 1.2246467991473532e-16], [-0.008726535498373897, -0.9999619230641713, 6.123233995736766e-17]]	[[1.2203421663297608e-16,-6.20858055762272e-17, -1.0], [0.9999756307053947, -0.006981260297961624, 1.2246467991473532e-16], [-0.006981260297961624, -0.9999756307053947, 6.123233995736766e-17]]	[[-1.523066994133026e-05,-0.0017452619091420732, 0.9999984769132877], [0.9999619230641713, -0.008726535498373997, 0.0], [0.008726522207103736, 0.9999604000354535, 0.0017453283658982615]]
10	47	47	47

Составлено авторами

В таблице 6 отражены виды , рассчитанные по данным обучаемым образцам (шаги III-IV).

Таблица 6

Виды, рассчитанные по обучаемым образцам


1	,,	-1, -1, -1	0, 1, 2
2	,,	-1, -1, -1	1, 0, 2
3	,, 0	-1, -1, -1	0, 2, 1
4	,,	-1, -1, -1	1, 0, 2

Составлено авторами

Таблица 7

Калибровочные базисы обучаемых образцов для вида 4

№
1	1978.0, 2628.480534115393	1978.0, 2630.784511712388	1977.9774044399742, 2628.480551626346
6	1	1	1
7	6.283185307179586, 3.1328660073298216, 1.5707963267948966	6.283185307179586, 3.134611336581816, 1.5707963267948966	6.281439977927592,-0.008726646259971771, 4.71238898038469
8	0.46364760900080610.6435011087932844	0.46364760900080610.6435011087932844	0.46364760900080610.6435011087932844
9	[[1.8369935141198218e-16, -1.0, -5.343461882864711e-19], [-0.9999619230641713, -1.8368769371258616e-16, -0.008726535498373959], [0.008726535498373959, 2.1373847531458845e-18, -0.9999619230641713]]	[[1.8369851206103478e-16,-1.0, -4.2747890389566373e-19], [-0.9999756307053947, -1.8369105111637583e-16, -0.006981260297961684], [0.006981260297961684, 1.7099156155826549e-18, -0.9999756307053947]]	[[-0.0017453283658986289, 0.9999984769132877, -1.6030385648594314e-18], [-0.9999604000354535, -0.0017452619091424405, -0.008726535498374058], [-0.008726522207103796, -1.5230669941331968e-05, 0.9999619230641713]]

Составлено авторами

При добавлении новых обучаемых образцов, виды 1-3 исключаются из списка видов и остаётся вид 4. Данный вид является одинаковым для любых тестовых изображений, снятых при тех же технических условиях съёмки.

В таблице 7 – калибровочные базисы для вида 4: показаны отличные параметры от первичных базисов (шаг V). Параметры 1 вычислены по формуле (5).


(а)	(б)
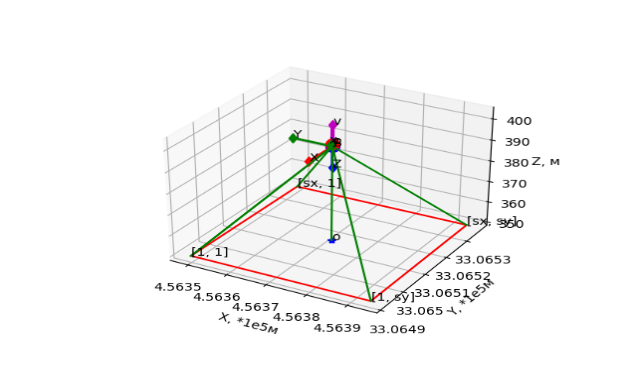
Рис. 9. Ракурс съёмки (а), в окрестности точки фотографирования (б) (для 1-го обучаемого образца вида 4)Составлено авторами

Для образца вида 4 показаны: на рисунке 8 – положение рассчитанной главной точки (параметр 1); на рисунке 9а – положение изображённой местности (полигон ) относительно камеры; на рисунке 9б – положение системы координат изображения относительно картографической системы координат.

Таблица 8

Калибровочный базис тестового образца

№	Обозначение	Значение
1		1975.4108014024496, 2640.0000001910935
2		3956, 5280
3	,	29.88916363888889, 98.54746502777778
4		[456305.3992197406, 3306589.8785657454, 394.384
5		44.996
6		0.01229
7		4.71238898038469, 3.139847324337799, 3.115412714809878
8		0.4636476090008061, 0.6435011087932844
9	A	[[0.02617694830787324, 0.9996558024107687, 0.001744730285457878],[0.9996573249755573, -0.0261769084381111, -4.5687370414385584e-05], [-3.206116195137692e-19, 0.0017453283658983227, -0.9999984769132877]]
10		47

Составлено авторами

В таблице 8 отражены для вида 4 параметры калибровочного базиса для произвольного тестового изображения датасета – ID DJI_20221115144415_0107_V, на рисунке 10а – тестовое изображение и положение рассчитанной главной точки (а), на рисунке 10б – рассчитанный ракурс съёмки (шаг VI).


(а)	(б)
Рис. 10. Изображение и главная точка (а), ракурс съёмки (на примере тестового образца для вида 4)Составлено авторами

Расчёт картографических и географических координат по матричным координатам производится по формулам (7)-(9). Например, точки A и B (см. рисунок 10а) имеют матричные координаты: . Отрезок AB образует сторону здания в основании. Если считать, что данные точки лежат на земле, то их аппликаты – высота поверхности Земли над уровнем моря. Тогда по формуле (9): ; . Отсюда длина отрезка: . Географические координаты точек: ; .

Выводы

В работе представлен алгоритм калибровки фотограмметрических параметров для возможности практического применения фотограмметрической модели преобразования двумерных координат точек снимка в трёхмерные координаты точек объекта. Условно введены понятия базиса изображения (набор необходимых фотограмметрических параметров изображения для расчёта трёхмерных координат) и вида (корректирование направления на изображаемую поверхность, заданного углами Эйлера).

Алгоритм включает следующие процедуры: извлечение первичного набора метаданных для обучаемых образцов; расчёт первичных базисов; расчёт видов по первичным базисам; на базе полученных видов расчёт калибровочных базисов образцов. Далее по тестовому изображению с теми же техническими характеристиками съёмочного оборудования рассчитывается калибровочный базис, по которому уже рассчитываются трёхмерные координаты по координатам матрицы изображения.

Литература

Михайлов А. П., Чибуничев А. Г. Фотограмметрия: Учебник для вузов / Под общ. ред. А.Г. Чибуничева. М.: Изд-во МИИГАиК, 2016. 294 с.
Козин Е. В., Карманов А. Г., Карманова Н.А., Фотограмметрия СПб: Университет ИТМО, 2019. 142 с. URL: https://books.ifmo.ru/file/pdf/2455.pdf.
Карманов А. Г. Фотограмметрия / Университет ИТМО, 2012. 171 с. URL: https://www.geokniga.org/bookfiles/geokniga-fotogrammetriya.pdf?ysclid=m0slhqtyzs409374700.
Краснопевцев Б.В. Фотограмметрия. М.: УПП “Репрография” МИИГАиК, 2008. 160 с.
Yasutaka Furukawa and Jean Ponce. Accurate camera calibration from multi-view stereo and bundle adjustment. International Journal of Computer Vision, 84(3):257–268 p.p., September 2009. URL: https://www.mindat.org/reference.php?id=6673055.
Alper Serhat Zeytunlu. Two-Dimensional Face Recognition Algorithms in the Frequency Domain / A Thesis in The Department of Electrical and Computer Engineering / Presented in Partial Fulfillment of the Requirements for the Degree of Master of Applied Science at Concordia University. Montreal, Quebec, Canada. January 2012.
В. В. Коротаева, А. В. Краснящиха, С. Н. Ярышева, Х. В. Нгуена. Метод автоматической калибровки системы / Научно-технический вестник информационных технологий, механики и оптики Scientific and Technical Journal of Information Technologies, Mechanics and Optics. 2014, № 4 (92).
Davide Scaramuzza. Vision Algorithms for Mobile Robotics. Lecture 03, Camera Calibration. URL: https://rpg.ifi.uzh.ch/docs/teaching/2021/09_multiple_view_geometry_3.pdf.
GitLab. URL: https://gitlab.com/jay_mccure/pyproj.
Общество защиты прав потребителей «Триумф» [Электронный ресурс]. Анатомия цифровой фотокамеры. Фокусное расстояние и эквивалентное фокусное расстояние. URL: https://potrebzashita.pro/poleznye-stati/anatomiya-tsifrovoj-fotokamery-fokusnoe-rasstoyanie-i-ekvivalentnoe-fokusnoe-rasstoyanie.
Бруевич П.Н. Фотограмметрия: Учеб. для вузов. М.: Недра, 1990. 285 с.
Лобанов А. Н. Фотограмметрии: Учебник для вузов. 2 с изд., перераб. И доп. М., Недра, 1984, 552 с.
Лурье И. К. Геоинформационное картографирование. Методы геоинформатики и цифровой обработки космических снимков : учебник. М.: КДУ, 2008. 424 с.
VirtualSurveyor [Электронный ресурс]. URL: https://support.virtual-surveyor.com/support/solutions/articles/1000310553-download-sample-datasets.


Richter A. A.1^,2, Chuklin S. I.^2,3	*Algorithm for calibration of photogrammetric parameters for calculating three-dimensional coordinates of image points*

	¹Tazmar IT Solutions Joint Stock Company, St. Petersburg²Scientific Research Institute of Aerospace Monitoring “AEROSPACE”, Moscow ³ St. Petersburg State University, St. Petersburg e-mail: ¹urfin17@yandex.ru

Abstract. The paper describes an algorithm for pre-calibration of photogrammetric parameters for the possibility of practical application of a photogrammetric model for converting “flat” coordinates of image points into corresponding three-dimensional coordinates of object points. The general scheme of the algorithm consisting of five steps is presented. To describe the procedures, the concepts of image basis (primary and calibrated) and type are conditionally introduced. The input data of the algorithm is a set of trained samples, each of which includes the image itself (with the necessary metadata) and their reference polygons (in the form of geographical coordinates of the image vertices). A calibration experiment was conducted using the example of a training set as part of a publicly available dataset. For an arbitrary test image in the dataset, photogrammetric parameters were calibrated and three-dimensional coordinates were calculated using the example of characteristic image points.

Keywords: calibration, photogrammetric parameters, three-dimensional c oordinates.

References

1. Mihajlov A. P., CHibunichev A. G. Fotogrammetriya: Uchebnik dlya vuzov / Pod obshch. red. A.G. CHibunicheva. M.: Izd-vo MIIGAiK, 2016. 294 s. (in Russian)

2. Kozin E. V., Karmanov A. G., Karmanova N.A., Fotogrammetriya SPb: Universitet ITMO, 2019. 142 s. URL: https://books.ifmo.ru/file/pdf/2455.pdf. (in Russian)

3. Karmanov A. G. Fotogrammetriya / Universitet ITMO, 2012. 171 s. URL: https://www.geokniga.org/bookfiles/geokniga-fotogrammetriya.pdf?ysclid=m0slhqtyzs409374700. (in Russian)

4. Krasnopevcev B.V. Fotogrammetriya. M.: UPP “Reprografiya” MIIGAiK, 2008. 160 s. (in Russian)

5. Yasutaka Furukawa and Jean Ponce. Accurate camera calibration from multi-view stereo and bundle adjustment. International Journal of Computer Vision, 84(3):257–268 p.p., September 2009. URL: https://www.mindat.org/reference.php?id=6673055.

6. Alper Serhat Zeytunlu. Two-Dimensional Face Recognition Algorithms in the Frequency Domain / A Thesis in The Department of Electrical and Computer Engineering / Presented in Partial Fulfillment of the Requirements for the Degree of Master of Applied Science at Concordia University. Montreal, Quebec, Canada. January 2012.

7. V. V. Korotaeva, A. V. Krasnyashchiha, S. N. YArysheva, H. V. Nguena. Metod avtomaticheskoj kalibrovki sistemy / Nauchno-tekhnicheskij vestnik