Геополитика и экогеодинамика регионов.
Том 9 (19). Вып. 2. 2023 г. С. 332–337.
УДК 57.033; 574.42
Т. И. Сулейманов1, Х. Г. Асадов2, Т. М. Тахмазов3
Обобщение модели роста Берталанфи для гетерогенной среды развития применительно к смешанному лесу
1,2,3 Национальное Аэрокосмическое Агентство, г.Баку, Азербайджанская Республика
e-mail:1 journal-anasa@yahoo.com, 2 asadzade@rambler.ru, 3 thmzovtbriz66@gmail.com
Аннотация. Показано, что классическая модель роста Берталанфи, разработанная для гомогенной среды , применима после некоторого обобщения также к неоднородной среде, в частном случае к неоднородному лесу, где деревья в лесу неоднородны по виду. Обобщение этой модели осуществляется следующим образом. Изменение статистики диаметра деревьев в смешанном лесу сопровождается изменением общего показателя роста, т.к. показатели роста разных видов деревьев различны. С учетом вышеизложенного в известную модель введены нормированные функциональные зависимости параметров известной модели от диаметра деревьев. Показано, что предложенная обобщенная модель Берталанфи для гетерогенной среды, представляющий собой некоторый функционал, имеет экстремум в виде минимума при некотором фиксированном виде зависимости одного из вновь введенных функциональных зависимостей.
Ключевые слова: смешанный лес, модель роста, диаметр, функционал, гетерогенная среда
Введение
Хорошо известно, что скорости процесса гибели и развития (роста) лесов зависит от типа деревьев и их размера [1-4]. Вместе с тем, существует единая обобщенная модель роста и гибели деревьев в виде [5]

Очевидно, что модель (2) может быть применен к одному типу дерева, т.к. две разные типы деревьев достигают равной величины диаметра на разных стадиях развития. Следовательно, возникает необходимость обобщения модели (2) к смешанному лесу. Ниже рассматривается предлагаемый метод обобщения модели роста Берталанфи применительно к смешанному лесу.
Таким образом, целью настоящей работы является разработка обобщенной модели роста на базе модели (2) применительно к процессу роста деревьев в лесу смешанного типа.
Материалы и методы
Исходным положением предлагаемой модели является то, что диаметры деревьев имеющихся в лесу составляют некоторое множество,

Таким образом, выражения (16)-(19) составляют основу предлагаемой обобщенной модели Берталанфи. Рассмотрим задачу оптимизации предложенной обобщенной модели роста.
Оптимизация модели роста
Конкретно рассмотрим задачу оптимального выбора функции 3( ), при которой функционал (16) достиг бы экстремального значения.
С учетом (16) и (19) составим задачу безусловной вариационной оптимизации. Целевой функционал этой задачи имеет вид:

Следовательно при решении (27) целевой функционал (20) будет иметь минимум.
В целом факт уменьшения функции роста при увеличении диаметра дерева в гомогенных лесах хорошо известно. В качестве примера на рис. 1 приведены кривые зависимости количества деревьев от диаметра этих деревьев [5].
Вместе с тем, если речь идет о гетерогенных лесах, где имеются деревья разных типов то возникает необходимость усовершенствовать модель (12). Проведенное исследование показало, что общий показатель развития при этом оказывается экстремальной величиной, экстремум которой зависит от типа взаимосвязи диаметра деревьев и одного из параметров модели Берталанфи.
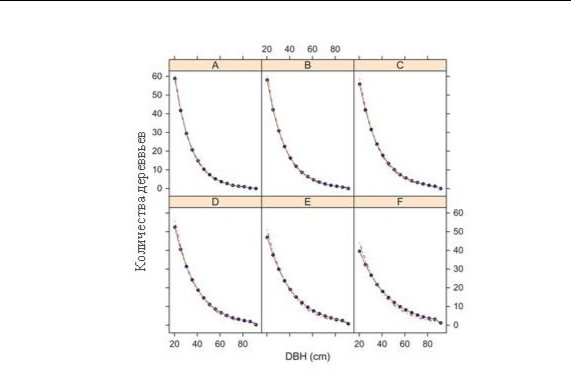
Рис. 1. Кривые зависимости количества деревьев от диаметра этих деревьев. Кривые составлены для шести разных лесных участков. Составлено авторами
Выводы
Сформулирована и решена задача обобщения модели роста Берталанфи для гетерогенной среды на примере смешанного леса. Показано, что классическая модель роста Фон Берталанфи применима к гомогенной среде, т.е. в данном случае к однородному леса. Если лес неоднородна, т.е. деревья в лесу неоднородны по виду, и если показателем роста взять диаметр дерево, то параметры этой модели должны быть изменены. Таким образом, изменение статистики диаметра деревьев в смешанном лесу сопровождается изменением общего показателя роста, т.к. показатели роста разных видов деревьев различны.
С учетом вышеизложенного в известную модель Берталанфи введены функциональные зависимости параметров этой модели от диаметра деревьев. Вновь введенные функциональные зависимости нормированы. Исследование показало, что предложенная обобщенная модель Берталанфи для гетерогенной среды, представляющий собой некоторый функционал, содержащий вновь введенные функциональные зависимости, имеет экстремум в виде минимума при некотором фиксированном виде зависимости одного из вновь введенных функциональных зависимостей.
Литература
- Richardson S. J., Smale M. C., Hurst J. M., Fitzgerald N. B., Peltzer D. A., Allen R. B., Bellingham P. J., McKelvey P. J. Large-tree growth and mortality rates in forests of the central North Island, New Zealand// Short communication.
- Crecente-Campo F., Soares P., Tome M., Dieguez-Aranda U. Modelling annual individual-tree growth and mortality of Scots pine with data obtained at irregular measurement intervals and containing missing observations// Forest Ecology and Management. 260. 2010. Pp. 1965-1974.
- Terra M. C., Lima M. G., Santos J. P., Cordeiro N. G., Pereira K. M., Dantas D., Calegario N., Botelho S. A. Nom-linear growth models for tree species used for forest restoration in Brazilian Amazon arc of deforestation// Brazilian Journal of Forestry Research. [Электронный ресурс]. Режим доступа: http://pfb.cnpf.embrapa.br/pfb/
- Sedmak R., Scheer L. Modelling of tree diameter growth using growth functions parameterized by least squares and Bayesian methods// Journal of forest science. 58. 2012. Pp. 245-252.
- Gove J. H. A demographic study of the exponential distribution applied to uneven-aged forests// Forestry. 2017. 90. Pp. 18-31. Doi:10.1093/forestry/cpw042
- Zhao-gang L., Feng-ri L. The generalized chapman-Richards function and applications to tree and stand growth// Journal of forestry research. 14(1). 2003. Pp. 19-26.
- Pienaar L. V., Turnbull K. J. The chapman-Richhards generalization of Von Bertalanffy’s growth model for basal area growth and yield in even-aged stands // For. Sci. 19. 1973. Pp. 2-22.
- Эльсгольц Л. Е. Дифференциальные уравнения и вариационное исчисление // М. Наука. 1974. Стр. 432.
- I. Suleymanov1, H. G. Asadov2, T. M. Tahmazov3
Generalization of the Bertalanfi growth model for a heterogeneous development environment in relation to a mixed forest
1,2,3 National Aerospace Agency, Baku, Republic of Azerbaijan e-mail:1 journal-anasa@yahoo.com, 2 asadzade@rambler.ru,
- thmzovtbriz66@gmail.com
Abstract. It is shown that the classical Bertalanfi growth model developed for a homogeneous medium is applicable, after some generalization, also to an inhomogeneous medium, in a particular case to an inhomogeneous forest, where the trees in the forest are heterogeneous in appearance. Generalization of this model is carried out as follows. The change in the statistics of the diameter of trees in a mixed forest is accompanied by a change in the overall growth rate, because the growth rates of different types of trees are different. Taking into account the above, normalized functional dependences of the parameters of the known model on the diameter of trees are introduced into the known model. It is shown that the proposed generalized Bertalanfi model for a heterogeneous medium, which represents a certain functional, has an extremum in the form of a minimum with some fixed form of dependence of one of the newly introduced functional dependencies.
Keywords: mixed forest, growth model, diameter, functional, heterogeneous environment
References
- Richardson S. J., Smale M. C., Hurst J. M., Fitzgerald N. B., Peltzer D. A., Allen R. B., Bellingham P. J., McKelvey P. J. Large-tree growth and mortality rates in forests of the central North Island, New Zealand// Short communication.
- Crecente-Campo F., Soares P., Tome M., Dieguez-Aranda U. Modelling annual individual-tree growth and mortality of Scots pine with data obtained at irregular measurement intervals and containing missing observations// Forest Ecology and Management. 260. 2010. Pp. 1965-1974.
- Terra M. C., Lima M. G., Santos J. P., Cordeiro N. G., Pereira K. M., Dantas D., Calegario N., Botelho S. A. Nom-linear growth models for tree species used for forest restoration in Brazilian Amazon arc of deforestation// Brazilian Journal of Forestry Research. URL: http://pfb.cnpf.embrapa.br/pfb/
- Sedmak R., Scheer L. Modelling of tree diameter growth using growth functions parameterized by least squares and Bayesian methods// Journal of forest science. 58. 2012. Pp. 245-252.
- Gove J. H. A demographic study of the exponential distribution applied to uneven-aged forests// Forestry. 2017. 90. Pp. 18-31. Doi:10.1093/forestry/cpw042
- Zhao-gang L., Feng-ri L. The generalized chapman-Richards function and applications to tree and stand growth// Journal of forestry research. 14(1). 2003. Pp. 19-26.
- Pienaar L. V., Turnbull K. J. The chapman-Richhards generalization of Von Bertalanffy’s growth model for basal area growth and yield in even-aged stands // For. Sci. 19. 1973. Pp. 2-22.
- El’sgol’c L. E. Differencial’nye uravneniya i variacionnoe ischislenie // M. Nauka. 1974. Str. 432. (in Russian)
Поступила в редакцию 01.04.2023 г.



